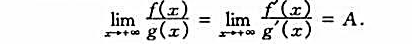题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
证明:恰有i个映射f;Ni-Ni使得(1)f(0)=0;(2)f为的同态(f具有以下形式f(x)=px(modi),p=0
证明:恰有i个映射f;Ni-Ni使得
(1)f(0)=0;
(2)f为 的同态(f具有以下形式f(x)=px(modi),p=0.1,2,...,i-1);
的同态(f具有以下形式f(x)=px(modi),p=0.1,2,...,i-1);
(3)以<N3+3>为例,给出所有满足(1),(2)要求的3个同态映射f;
(4)给出所有满足f(0)=0的<N3+3>到的同态f;
(5)给出所有满足f(0)=0的<N3+3>到的同态f.
 答案
答案





 .
.![设f(x)∈C[0,1],在(0,1)内可导,f(0)=0,f(1)=1,且f(x)在[0,1]上严](https://img2.soutiyun.com/ask/2020-12-04/975948781534127.jpg)
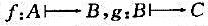 是映射,又令
是映射,又令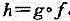 ,证明:
,证明: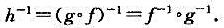
 .(ii)若
.(ii)若 ,则F是有界闭集.
,则F是有界闭集.
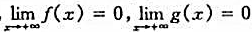 ,情形时的罗比达法则.
,情形时的罗比达法则.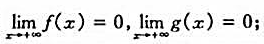
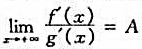 (A为实数,也可为±∞或∞)则
(A为实数,也可为±∞或∞)则